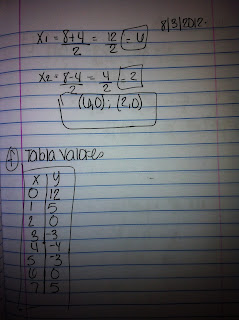Isaac Newton
         
(25 de diciembre de 1642 – 20 de marzo de 1727; 4 de enero de 1643  – 31 de marzo de 1727) fue un fisico, filosofo, teologo, inventor, alquimista y matematico ingles, autor de los Philosophiae naturalis principia mathematica , más conocidos como los Principia, donde describió la ley de gravacion universal y estableció las bases de la mecan medianteica clasica las leyes que llevan su nombre. Entre sus otros descubrimientos científicos destacan los trabajos sobre la naturaleza de la luzy la optica (que se presentan principalmente en su obra opticks) y el desarrollo del calculo matematico.

Funcion Cuadratica; Formula General y Estandar.

Funcion Cuadratica 

Formula General --> f(x)= ax^2+bx+c

Formula Estandar-->f(x)= a(x+h)^2-k

para realizar el ejercicio se necesita buscar 7 cosas :

a.vertice

b.concavidad

c.eje de simetria

d.intercepto en y (x=0)

e.intercepto en x (y=0)

f.tabla de valores 

g.grafica

Ceros y multiplicidades

Encuetre una funcion cuyos ceros son : 2,3

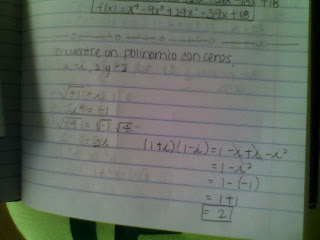
multiplicidad 2 : 1, 2

3 : 1 , 3

x1 = 2 => x-2

x2 = 3 => x-3

x3 = 3 =>x-3

x4 = 1 => x-1 f(x) = ( x-2 ) (x-3)^2(x-1)

= (x-2) (x^2-(3x)+3^2)x-1

= (x-2) (x^2-6x+9) (x-1)

= (x^3-6x^2+9x-2x^2+12x-18)(x-1)

= x^4-x^3-8x^3+21x^2-21x-18x+18

f(x)=x^4-9x^3=29x^2-39x+18

Encuentre un polinomio con ceros

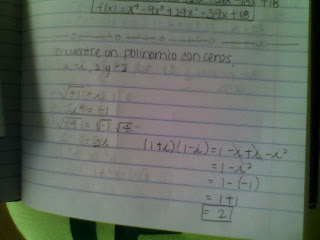
Por : monica medina

Funcion Cuadratica

Funcion Cuadratica

Una funcion cuadratica es una funcion que puede ser escrita en la forma :

f(x)=a(x-h)^2+k(a "no identico" o )

** La grafica de una funa cuadratica tiene forma de V y se conoce como una parabola..

Vertice de una parabola

* Si una parabola abre hacia arriba, tiene un punto minimo

* Si una parabola abre hacia abajo, tiene un punto maximo

* Este punto mas bajo o mas alto es el vertice de la parabola

* La forma del vertice de una funcion cuadratica es : f(x)=a(x-h)^2+k

*El vertice de la parabola es (h,k)

Por : Monica Medina

Funciones Inversas

Funciones Inversas (f ^-1 (x))

Sea F una funcion uno a uno con dominio A y rango B. Entonces su funcion inversa f^-1 tiene dominio B y rango A y esta definida por : f^-1 (y)= x <===> f(x)= y

Ejemplo f(x)= 3x - 5

1) Intercambie f(x) por y

y= 3x-5

2) Intercambie la x con la y

x= 3y-5

3) Despejar para Y

x= 3y-5

x + 5/ 3 = 3Y/3

x + 5/ 3 = Y

4) Intercambie Y por f^-1 (x)

f^-1(x)= x + 5 /3

(f o f^-1) (x)= 3(x+5/3) - 5

= x + 5 - 5

(f o f^-1) (x)= x

Ejemplo

2) f(x) = 1/ x +2

a) y= 1 /x + 2

(y + 2) x = 1/ y +2 (y+2)

xy + 2x = 1

xy/x= 1- 2x/x

y= 1 - 2x/x

f^-1(x)= 1 - 2x/x

3) f(x)= 6-4x

y= 6 -4x

x= 6 - 4y

x-6/-4 = -4y/-4

x-6/-4= 4

f^-1(x)= x-6/-4

Composicion de funciones

Dadas dos funciones f y g, la funcion compuesta f o g (denominada, tambien la composicion de f o g) esta definida por:
(f o g)(x)= f(g(x))


El dominio de f o g es el conjunto de todas las x en el dominio de g tal que g(x) esta en el dominio de f. En otras palabras (f o g)(x) se define siempre que g(x) y f(g(x)) esten definidas:
ejemplo: Sea f(x)= x^2
g(x)=x-3


Encuentre:

1. (f o g)(x)= f(g(x))
= f(x-3)^2
= (x-3)(x-3)
(f o g)(x)=X^2-6x+9

2. (g o f)(x)= g(f(x))
= X^2-3
(g o f)(x)= X^2 -3

3. (f o g)(5)= f(g(5))
= (5-3)^2
= 2^2
(f o g)(5)= 4

4. (g o f)(7)= g(f(7))
= 7^2 -3
=49-3
(g o f)(7)= 46

5. (f o f)(x)= f(f(x))
= f(x^2)
= (x^2)^2
(f o f)(x)= X^4

6. (g o g)(x)= g(g(x))
= g(x-3)
= (x-3)-3
(g o g)(x)= x-6


f(x)= 2x^2 -3x
g(x)=x + 1

1. (f o g)(x)= F(g(x))
= 2(x+1)^2 -3(x+1)
= 2(x^2 + 2x +1) -3x-3
= 2x^2 + 4x +2 -3x-3
= 2x^2 + x -1

2. (g 0 f)(x)= g(f(x))
= 2x^2 - 3x +1


3. (f o f)(x)= f(f(X))
= 2(2x^2-3x)^2 -3(2x^2-3x)
= 2(4x^4-12x^3+9x^2) -6x^2 +9x
= 8x^4 -24x^3 +18x^2-6x^2 +9x
= 8x^4 - 24x^3 +12x^2 +9x


hecho:paola roman

Operaciones con funciones

-suma : f(x)+g(x)= (f+g)(x)

-resta : f(x)-g(x)= (f-g)(x)

-multiplicacion : f(x) * g(x)= (fg)(x)

-division : f(x)/g(x)= (f/g)(x); g(x)=0

g(x)/f(x)= (g/f)(x); f(x)=0

Ejemplo 1 . f(x)= 2x-4

g(x)= x-2

a.suma : (f+g)(x)=2x-4+x-2

=3x-6

b.resta : (f-g)(x)=2x-4-(x-2)->2x-4-x-2

=x-2

c.multiplicacion : (f *g )(x)=2x-4 * x-2

=2x2-4x-4x+8

=2x2-8x+8

d.division : (f/g)(x)= 2x-4/x-2

=2(x-2)/x-2

=2

Ejemplo 2. : f(x)=7x2+x

g(x)0=2x

hallar :

a.(f+g)(x)=7x2+x+2x

=7x2 + 3x

b.(f-g)(x)=2x-(7x2 + x)

=2x-7x2-x

= -x-7x2

c.(fg)(x)=(7x2+x)(2x)

=14x3 + 2x2

d.(f/g)(x)=7x2+x/2x

=x(7x+1)/2x

=7x+1/2

e.(g/f)(x)=2x/7x2+x

=2x/x(7x+1)

=2/7x+1

POR : Cherina Capella

Trazado de graficas

A. Desplazamieno Vertical
y=f(x)+c
* Si c > o , la grafica se mueve c unidades hacia arriba.
* Si c < o , la grafica se mueve c unidades hacia abajo.

ejemplos :

#1 f(x)=x^2

f(x)=x^2+2

#2 f(x)=x^3

f(x)=x^3-2

#3

f(x)=√x)

f(x)=√x)+3

#4

f(x)=√x)-3

#5

f(x)=1/x

f(x)=1/x+2

B. Desplazamiento Horizontal

(no respeta signos)

y=f (x+k)

*Si K >O , la grafica se mueve K unidades hacia la izquierda

*Si K

Ejemplos :

#1

f(x)=x^2

f(x)=(x+2)^2

#2

f(x)=√x+2)-3

#3

f(x)=(x-3)^2+2

f(x)=x-2+3

C. Reflejos

Eje de x

y=-f(x)

Ejemplos :

#1 f(x)=-x^2

#2

f(x)=-x^3

#3

f(x)=-x

#4

f(x)=-√x)

#5

f(x)=-1/x

#6

f(x)=-^3√x)

por: monica medina

Dominio de Funciones

A menudo el dominio de una funcion no aparece especificando; la funcion aparece indicada por una ecuacion en dos variables.

- En este caso : Df= {x E R / Y= f (x) E R}

Es decir, el dominio de la funcion f es el conjunto mayor de numeros reales, tales que el valor resultante f(x) es un numero real (conjunto de valores de x)

Determine el Dominio de las siguientes funciones

1. f(x) = x2

¿Que valores puede asumir x de manera que el valor que resulte sea real?

f(5)= (5)^2 = 25

f(-3)= (-3)^2 = 9

f(1/2)= (1/2)^2

*Df= {x/x E/R}

Ejemplo 2

f (x)= 9 +x

Preguntemonos ¿ Que valores debe asumir el radicando para la raiz cuadrada sea un numero real?

2 Restricciones para sacar el dominio de la funcion

* no puede haber negativos dentro de un radical

* no puede haber 0 el denominador de un fraccion

Ejemplo 3

f(x)= 1 / 2- x

Ejemplo 4

f(x)= 9 +x / 2-x

Df= [-9,2) U (2 , infinito)

Rango de una funcion

- El rango, alcance, campo de valores es el conjunto de todos los resultados (y) que surgen al evaluar la funcion en los elementos del dominio (conjunto de valores de y )

f(x)=x^2

Af= [0, infinito)

Rf= [0, infinito)

Graficas de funciones Basicas

1. funcion de identidad f(x)=x






2. funcion lineal
F(x)=mx+b








3. funcion cuadratica
f(x)=x^2













4. funcion cubica
f(x)=x^3







5. funcion valor absoluto
f(x)= /x/











6. funcion de raiz cuadrada
f(x)= x^(1/2)














7. funcion racional
f(x)= 1/x











8. funcion constante
f(x)=b










9. funcion raiz cubica
f(x)=X^(1/3)

















Evaluacion de funciones

f(x)=x^2-4x+2

1. f(3)= 3^2-4(3)+2
= 9-12+2
f(3)= -1

2. f(1/2)= (1/2)^2 -4(1/2)+2
= 1/4 -2+2
f(1/2)= 1/4

3. f(a)= a^2 -4a+2


4. f(x+2)= (x+2)^2 -4(x+2)+2
= x^2 +4x+4-4x-8+2
f(x+2)= x^2-2


hecho por: paola roman